

The instantaneous angular velocity is the rate at which a particle moves in a circular path at a particular moment of time. Instantaneous velocity Velocity at any instant of time. T i = Initial time Average velocity is total distanceĭivided by the total time taken. Instantaneous velocity = limit as change in time approaches zero (change in position/change in time) = derivative of displacement with respect to timeĪverage velocity and instantaneous velocity formula Formula Symbol Definition Average velocity s f= Final displacement It is called instantaneous velocity and is given by the equation v = ds/dt. Instantaneous velocity formula calculusīy using calculus, it is always possible to calculate the velocity of an object at any moment along its path. The above derivative holds a finite value when both the denominator and the numerator tend to zero.
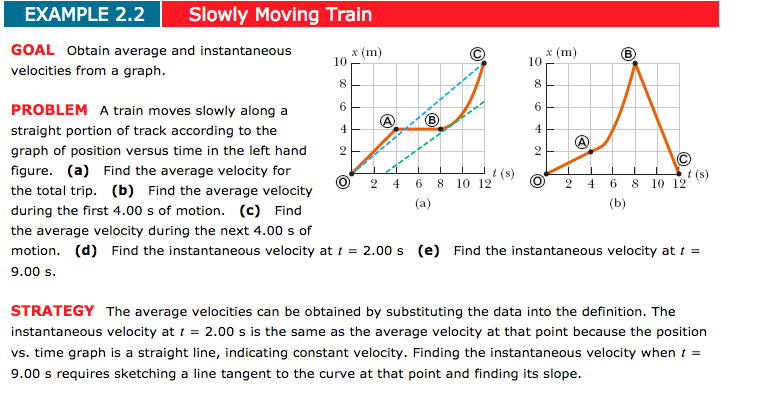
Here, ds/dt is the derivative of displacement (s) with respect to time (t). In mathematical terms, we can write the instantaneous velocity formula as, Since these numbers are approximately equal to 2, we can say that 2 is A’s slope. In the example, as we move B closer to A, we get values of 1.7, 1.8, and 1.96 for K. Here we can use the points (4,7.7), (3.5, 6.90), and (3.25, 6.49) for B and the original point of (3,6) for A.Ĭalculate the slope for an infinitely small interval on the tangent line.If we consider the limit of the function at that point, we will get the value of the slope at that point.Keep choosing points closer to one another then, it will begin to approach the slope of the tangent line.Repeat to find slope several times, moving B nearer to A. To find the derivative of a given displacement equation, differentiate the function with respect to time, Consider the derivative of the given equation. It means the equation must contain the variable ‘ s‘ on one side and ‘ t‘ on the other side, To calculate instantaneous velocity, we must consider an equation that tells us its position ‘s’ at a certain time ‘t’. Consider an equation for velocity in terms of position/displacement.
#Distance vs time graph physics instantaneous velocity how to#
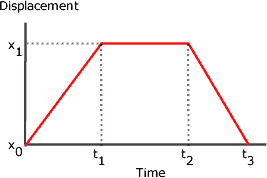
To know how to calculate instantaneous velocity of an object, we have steps to follow. i.e., the derivative of displacement (s) with respect to time(t) taken. To Calculate V inst we can use the displacement-time graph/ Instantaneous Velocity Formula. Instantaneous velocity is taken as the limit of average velocity as the time tends towards zero. If this tangent slopes towards the right then instantaneous velocity would be considered positive this is because of the positive value of the slope on the other hand if the tangent slopes downward to the right then the instantaneous velocity would be considered negative, because of negative slope.Instantaneous velocity tells us about the motion of a particle at a specific instant of time anywhere along its path.

The slope of this tangent would give the value of instantaneous velocity corresponding to the point \(S\). In the limiting stage, the chord \(RS\) would become the tangent to the curve. When \(\Delta t\) approaches the zero the point \(R\) approaches point \(S\). It is clear from this figure that the average velocity of the particle between points \(R\) and \(S\) is given by the relation \ The slope of the straight line joining two points on the position-time graph gives the average velocity of the particle between these two points.Ĭonsider the figure given below which shows a position-time graph of a body moving with variable velocity. How to find instantaneous velocity on a position-time graphīefore going any further I would like to advise you to read this article on How to find average velocity on a position-time graph. It tells us about how fast an object is moving anywhere along its path. We are interested in the instantaneous velocity of the particle when the particle is moving with variable velocity along its path. The instantaneous velocity of a particle is the velocity of the particle at any instant of time or at any point on its path. In this article, we will learn how to find instantaneous velocity on a position-time graph.įirst of all, let us look at the definition of instantaneous velocity.


 0 kommentar(er)
0 kommentar(er)
